Page 8 - English Class X_cbse new (FINAL).cdr

S. Solution Marking S. Solution Marking
No. Scheme No. Scheme

8. Resultant dipole moment [1] 11. Representation of electric field: The electric field due to a positive
charge (+q) is represented as
pr = p12 + p22 + 2p1p2 cos120
= 2p2 + 2p2 cos120

( )=  1 2p2 − p2 = p,
2p2 + 2p2 ×  − 2 =

Using law of addition of vectors, we can see that the resultant dipole [1]
makes an angle of 60° with the y axis or 30° with x - axis.

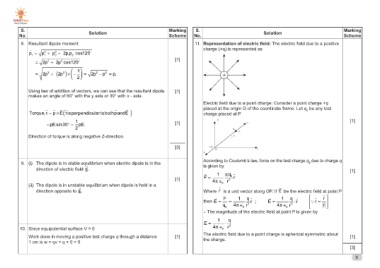
( )Torque,τ = p × E τ isperpendicular tobothpandE Electric field due to a point charge: Consider a point charge +q
placed at the origin O of the coordinate frame. Let q0 be any test
= pE sin30° = 1 pE. charge placed at P.
2
[1] [1]
Direction of torque is along negative Z-direction. [3]

9. (i) The dipole is in stable equilibrium when electric dipole is in the According to Coulomb’s law, force on the test charge q0 due to charge q [1]
direction of electric field E. is given by
[1]
(ii) The dipole is in unstable equilibrium when dipole is held in a [1] F = 1 q q0 r [3]
direction opposite to E. 4π ∈0 r2
6
Where r is a unit vector along OP. If E be the electric field at point P

then E= F = 1 q r ; E = 1 q ⋅r ∵ r = r 
q0 4π ∈0 r2 4π ∈0 r3  r 

∴ The magnitude of the electric field at point P is given by

E = 1 ⋅ q
4π ∈0 r2
10. Since equipotential surface V = 0
[1] The electric field due to a point charge is spherical symmetric about
Work done in moving a positive test charge q through a distance
1 cm is w = qv = q × 0 = 0 the charge.