Page 13 - English Class X_cbse new (FINAL).cdr
P. 13
S. Solution Marking S. Solution Marking
No. Scheme No. Scheme
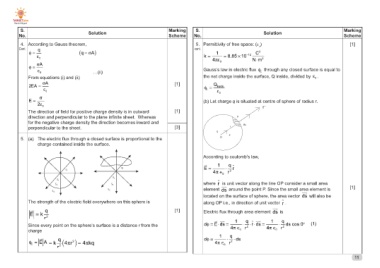
4. According to Gauss theorem, [1] 5. Permittivity of free space: (εo) [1]
[1]
Cont. φ = q (q = σA) [3] cont. 1 C2
ε0 4πε0 N ⋅ m2
k = = 8.85 × 10−12
φ = σA Gauss’s law in electric flux φE through any closed surface is equal to
ε0 …(ii) the net charge inside the surface, Q inside, divided by ε0 .
From equations (i) and (ii) φE = Qinside
2EA = σA ε0
ε0
E= σ (b) Let charge is situated at centre of sphere of radius r.
2ε0
E
The direction of field for positive charge density is in outward q P
direction and perpendicular to the plane infinite sheet. Whereas O r ds
for the negative charge density the direction becomes inward and r
perpendicular to the sheet.
5. (a) The electric flux through a closed surface is proportional to the
charge contained inside the surface.
According to coulomb’s law,
qq E = 1 ⋅ q r
4π ∈0 r2
S1 S1 where r is unit vector along the line OP consider a small area [1]
S2 element ds around the point P. Since the small area element is 11
S2 located on the surface of sphere, the area vector ds will also be
S3 S3
along OP i.e., in direction of unit vector r .
The strength of the electric field everywhere on this sphere is
E = k q [1] Electric flux through area element ds is
r2
1 q 1 q (1)
Since every point on the sphere’s surface is a distance r from the dφ = E ⋅ ds = 4π ∈0 ⋅ r2 ⋅ r ⋅ ds = 4π ∈0 ⋅ r2 ds cos 0°
charge
( )φE q dφ = 1 ⋅ q ⋅ ds
= E A = k r2 4πr 2 = 4πkq 4π ∈0 r2