Page 5 - English Class X_cbse new (FINAL).cdr

Sub Topic: 1.2

S. Solution Marking S. Solution Marking
No. Scheme No. Scheme

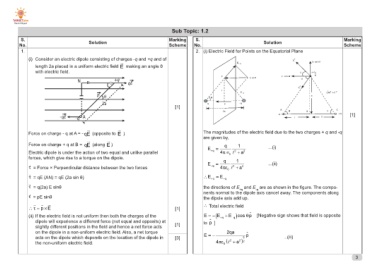
1. 2. (i) Electric Field for Points on the Equatorial Plane

(i) Consider an electric dipole consisting of charges -q and +q and of

length 2a placed in a uniform electric field E making an angle θ
with electric field.

N +q qE

pθ [1]
2a
[1]
-qE -q A [1] [1]
[3]

Force on charge - q at A = - qE (opposite to E ) The magnitudes of the electric field due to the two charges + q and -q
are given by,

Force on charge + q at B = qE (along E ) E+q = q 1 ...(i)
4π ∈0 2 + a2 ...(ii)
Electric dipole is under the action of two equal and unlike parallel
forces, which give rise to a torque on the dipole. E−q = q 1
4πε0 2 + a2
τ = Force × Perpendicular distance between the two forces
∴E+q = E−q
τ = qE (AN) = qE (2a sin θ)
the directions of E and E are as shown in the figure. The compo-
τ = q(2a) E sinθ +q -q
nents normal to the dipole axis cancel away. The components along
τ = pE sinθ
the dipole axis add up.

∴τ = p×E ∴ Total electric field

(ii) If the electric field is not uniform then both the charges of the ( )E = − E+q + E−q cos θp [Negative sign shows that field is opposite
dipole will experience a different force (not equal and opposite) at
slightly different positions in the field and hence a net force acts to p ]
on the dipole in a non-uniform electric field. Also, a net torque
acts on the dipole which depends on the location of the dipole in E = − 2qa )3 p ..(iii)
the non-uniform electric field. 2
4πε0 ( 2+ a2

3