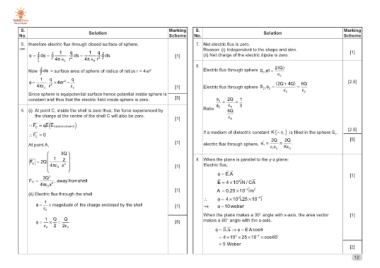
Page 14 - English Class X_cbse new (FINAL).cdr

S. Solution Marking S. Solution Marking
No. Scheme No. Scheme

5. therefore electric flux through closed surface of sphere, [1] 7. Net electric flux is zero. [1]
Reason: (i) Independent to the shape and size.
cont. 1 q 1 q (ii) Net charge of the electric dipole is zero.
4π ∈0 r2 4π ∈0 r2
φ = dφ = ⋅ ds = ds

∫ ∫ ∫s

∫Now ds = surface area of sphere of radius of ratius r = 4πr2 8. Electric flux through sphere S1,φ1 = 2(Q)

1 q q ∈0
4πεo r2 εo
φ= ⋅ × 4πr2 = S2,φ2 = (2Q + 4Q) = 6Q [2.5]
ε0
[1] Electric flux through sphere ε0
[5]
Since sphere is equipotential surface hence potential inside sphere is φ1 = 2Q =1
constant and thus that the electric field inside sphere is zero. φ2 3
ε0
6. (i) A t point C, inside the shell is zero thus, the force experienced by Ratio 6Q
the charge at the centre of the shell C will also be zero.
[1] ε0
( )∵ FC = qE Einsidetheshell=0
[1] If a medium of dielectric constant K {= εr } is filled in the sphere S1, [2.5]
∴ FC = 0 [5]
[1] 2Q 2Q .
At point A, electric flux through sphere, φ1' = εr ε0 = Kε0
[1]
 3Q  [1]
[5]
FA = 2Q  1 2 9. When the plane is parallel to the y-z plane:
 4πε0 x2  Electric flux,
 
φ = E.A
FA = 3Q2 , away fromshell E = 4 × 103 iN / CA [1]
4πε0 x2 A = 0.25 × 10−2 im2
∴ φ = 4 × 103 i.25 × 10−4 i [1]
(ii) Electric flux through the shell ⇒ φ = 10 weber [2]

φ = 1 × magnitude of the charge enclosed by the shell When the plane makes a 30° angle with x-axis, the area vector 12
ε0 makes a 60° angle with the x-axis.

φ= 1 ×Q= Q φ = Ε.Α ⇒ φ = E A cosθ
ε0 2 2ε0 = 4 × 103 × 25 × 10−4 × cos 60
= 5 Weber